本帖最后由 bclxx 于 2012-7-24 23:40 编辑
好几年前收集在电脑里头,要是出现版权问题,请删帖。
电脑鼠的英文名称为Micromouse,实际上是一个由微处理器控制的,集感知、判断、行走功能于一体,能够自动寻找最佳路径到达目的地的小型机器人。它可以在“迷宫”中自动感知并记忆迷宫地图,通过一定的算法,寻找一条最佳路径,以最快的速度到达目的地。1997年,在美国举办了第一届电脑鼠竞赛,随后,电脑鼠竞赛传入欧洲,首届欧洲电脑鼠竞赛于1980年在伦敦举办,之后英国的电脑鼠比赛便由电子工程协会(IEE)主办。1980年11月日本电脑鼠协会(JMA)在东京举办了第一届竞赛,此后,日本每年都要举办一届电脑鼠竞赛。我国台湾也于1986年10月举办了首届电脑鼠比赛。现在国际电工和电子工程学会(IEEE)每年都要举办一次国际性的电脑鼠走迷宫竞赛,各国选手报名踊跃,主要是大学生,为此部分大学还开设了“电脑鼠原理和制作”选修课程。 由于电脑鼠要由参赛选手自己设计制作,不仅要求选手具有嵌入式系统应用﹑传感器﹑控制技术等多方面的知识、经验和实践能力,还要求具有编写寻找最佳路径算法的能力。由于迷宫路径设置是随机的,因而竞赛难度较大,极富挑战性。这对培养和提高学生的创新精神和实践能力,有着深远的意义。2007年5月— 8月将举办由我国部分地区(上海及长三角地区)参加的首届电脑鼠邀请赛。 1 电脑鼠走迷宫的规则 有关电脑鼠国际比赛的详细规则,可参阅国际电工和电子工程学会(IEEE)的官方网站:http://www.eece.maine.edu/sc2006/2006MicromouseRules.pdf 。 迷宫的规格 迷宫由256个方块(单元)组成,每个方块的大小为18厘米见方,排成16行×16列。迷宫的隔墙板沿方块的四周布设,形成迷宫通道。隔墙板高5厘米﹑厚1.2厘米,因此迷宫通道的实际宽度是16.8厘米。隔墙板的两个侧面是白色的,顶部是红色的。迷宫的地板由木质材料做成,涂上没有反光的黑漆。隔墙板的侧面和顶部对红外线有反射特性,而地板则对红外线有吸收特性。竞赛起始点可设在迷宫的任何一角,其三面要有隔墙;竞赛的终点设在迷宫的中央,有四个方块那么大小。图一为一个实际的电脑鼠竞赛用的迷宫照片。
图一电脑鼠竞赛用的迷宫照片
1.2 电脑鼠的规格 电脑鼠要求由参赛者自制,使用电源为能源,不能使用其它可燃物为能源。电脑鼠结构高出隔墙部分的长宽几何尺寸应不大于25×25厘米,对高度没有限制。一个完整的电脑鼠应包含有机身、电源、传感器、微处理器、马达及驱动等部分。电脑鼠的传感器可分为三组,分别用来感知前、左、右三个方向是否已靠近宫壁,并将所获得信息传送给微处理器进行处理。微处理器要完成多种信息的处理,如路径、迷宫地图、行走距离、马达控制等,并要能够作出判断。在马达的控制下,电脑鼠能够完成直行、转弯、掉头以及加减速等动作。通常采用左右独立的马达驱动和控制,以使微处理器的控制更加灵活。图二为一个实际参加竞赛的电脑鼠样例照片。 
图二电脑鼠样例照片。1.3 竞赛的规则 电脑鼠的基本功能是从起点开始走到终点,这个过程称为一次“运行”,所花费的时间称为“运行时间”。从终点回到起点所花费的时间不计算在运行时间内。电脑鼠从第一次激活到每次运行开始,所花费的时间称为“迷宫时间”。如果电脑鼠在比赛时需要手动辅助,这个动作称为“碰触”。竞赛使用这三个参数,即运行时间﹑迷宫时间和碰触,从速度﹑求解迷宫的效率和电脑鼠可靠性三个方面来进行评分。 电脑鼠的得分是通过计算每次运行的“排障时间”来衡量的。所谓排障时间是这样计算的:先将迷宫时间的1/30加上一次运行时间,如果这次运行结束以后电脑鼠没有被碰触过,那么还要再减去10秒的奖励时间,这样得到的就是排障时间。电脑鼠在迷宫中的停留或运行的总时间不可超过15分钟,在限时内允许运行多次,允许取其中最短的排障时间作为参赛的计分成绩。当然,排障时间越短越好 例如:一个电脑鼠在迷宫中运行时间为4分钟(240秒)没有碰触过,迷宫时间使用了20秒,这次运行的排障时间就是:20秒+(240秒×1/30)- 10秒 = 18秒。 电脑鼠在迷宫通道内行走时不能碰到隔墙板,遇到岔道口时要能够自动作出方向选择。本文规定:如果进入迷宫是为了进行探测和记忆,这次运行就称为“试跑”;如果进入迷宫是根据先前的记忆和经验,按照智能算法确定最佳路径,并以最快的速度到达目的地,这次运行就称为“冲刺”。 2 电脑鼠走迷宫的算法 2.1 探测策略 电脑鼠走迷宫可以采用全迷宫探索策略,即将迷宫的所有单元均搜索一次,从中找出最佳的行走路径。这种策略需要有足够的时间或探测次数,但在IEEE竞赛规则中每场竞赛只有15分钟的时间,因此是不可能的。另一种方法是部分迷宫探索策略,即在有限的时间或探测次数下,只探测迷宫的一部分,从中找出次最佳的路径,显然只能采用这种策略。 电脑鼠在一巷道内行走,如果最后无路可走,则该巷为死巷。电脑鼠在任一单元内,可能的行走方向最多只有三个(前、左、右),如果有二个或二个以上的可能行走方向,称为交叉,遇有交叉时,由于有多个可以行走的方向,在行走方向的选择上,可有下面的几种选择法则: Ÿ 右手法则:遇有交叉时,以右边为优先的前进方向,然后是直线方向、左边方向。 Ÿ 左手法则:遇有交叉时,以左边为优先的前进方向,然后是直线方向、右边方向。 Ÿ 中左法则:遇有交叉时,以直线为优先的前进方向,然后是左边方向、右边方向。与此类似的还有中右法则。 Ÿ 乱数法则:遇有交叉时,取随机值作为前进方向。 Ÿ 向心法则:由于终点在迷宫的中心,遇有交叉时,以向迷宫中心的方向为优先的前进方向。 2.2 标记 为了记忆迷宫的详细信息,需要对迷宫单元的位置进行线路标记。全迷宫共有16×16个单元组成,可采用二维坐标方式标记,即用每个单元的XY坐标表示,如起点可标记为(0,0),终点为(7,7)。此外,还需要对迷宫单元的可行进方向进行标记,可采用绝对方位或相对方位二种方式。 绝对方位:这是一种与电脑鼠行进方向无关的标记方式,以一个四位的二进制数,分别表示“东”﹑“西”﹑“南”和“北”四个方向。以1表示允许行进(无墙壁),0表示不允许行进(有墙壁)。 相对方位:这是一种与电脑鼠行进方向有关的标记方式,以一个三位的二进制数即可实现标记,分别表示“前”“左”“右”, 以1表示允许(无墙壁),0表示不允许(有墙壁)。 2.3 阻断 在电脑鼠试跑过程中或在最后冲刺时,需要对部分路径进行“阻断”,即在发现某条路径是死路(只有入口而无出口)时,在该路径的入口处(一般是交叉点)设置标记,即将入口的线路标记由1改为0。 2.4 试跑 试跑是获得迷宫地图(各单元路线标记)的唯一方法,因而应在规则允许的情况下,尽可能多的获得迷宫信息,为最后的冲刺准备尽可能多的信息。在试跑过程中,要对经过的单元进行线路标记,同时还要选择一个合适的探测策略。 下面以1/4迷宫为例进行说明。假设迷宫图布局如图三所示,共有8×8=64个单元,起点在左下角(Start),终点在右上角(End)。选用一个8×8的矩阵map保存迷宫地图信息,矩阵的每个元素为1个字节,高4位表示探测到的可行进路径,以绝对方位标记,次序为“北”﹑“东”﹑“西”﹑“南”。低4位记录自起点的交叉点的个数。探测策略采用右手法则,在初始状态,矩阵map各元素的值均为FFH,00H表示死巷。 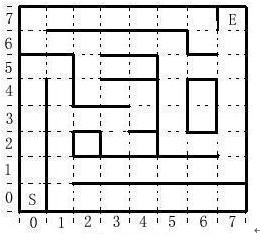
图三 1/4迷宫在探测过程中,如果下一个可行进的单元已经探测过(对应的矩阵元素值非00H或非FFH),只有在发现死巷时,才对map中的数据进行修改。对于其它情况,无论探测结果与矩阵中对应元素存储的信息是否一致,均不修改存储的信息。对于复杂的迷宫,往往不能仅使用一种探测策略,而要综合考虑,如增加向心法则。当发现交叉点时,应将该单元坐标和线路特征保存(如入栈),再分析可行的下一个单元是否已经探测过,如果均未探测过,则根据探测策略,选择一方向进行探测。如果部分单元已经探测,则选择未被探测的单元进行探测。遇有死巷,应返回最近的交叉点,同时将死巷阻断,修改入口单元的相应数值。 图四为首次探测时电脑鼠的行走路线示意,电脑鼠在探测过程中,将获得行走过的各单元的线路特征,表一为电脑鼠探测到(5,0)单元时的二维表(以十六进制表示,高4位为线路标记,低4位为交叉点数)。 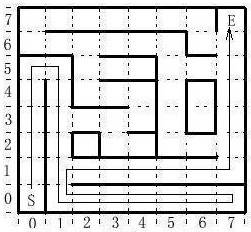
图四 首次探测行走路线 表一 探测到(5,0)时的map二维表 从图四可以看出,该巷为一死巷,当电脑鼠探测到(7,0)时,发现是死巷,将按原路返回到最近的交叉点(1,1),进行阻断,即将向“南”修改为不可行,并修改交叉点的数据,由原值B2H改为90H,死巷中的数据全写零,并继续完成探测,最后得表二 。 表二 执行阻断后的二维表 根据IEEE电脑鼠竞赛规定,当电脑鼠到达终点后,可进行返回探测,从而获得更多的迷宫地图信息。图五为返回探测时的行走路径。在返回探测中,未发现死巷,返回起点,探测后的结果如表三。 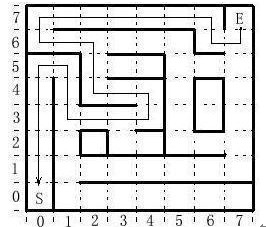
图五 返回时的探测路径表三 返回探测后的二维表 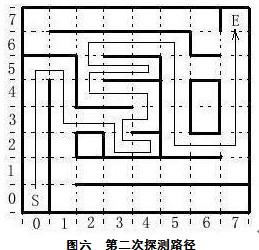
图六 第二次探测路径 第二次探测如图六,在(3,3)和(2,5)分别执行阻断,将获得二维表四 表四 第二次探测后的二维表 2.5 数据补全 由于不可能将所有的单元均探测到,在有了一定的数据基础上,就可以实现数据补全了。数据补全,就是对未探测到的单元,通过周围已有的相数据,可进行补充的一种方法。方法是寻找单元数据为FFH的单元,如果该单元的“东”﹑“西”﹑“南”﹑“北”四个相邻的单元均为非00H或FFH,分析“东”﹑“西”和“南”﹑“北”四个单元的二组数据,看是否有指向该单元的可行方向,如果有,在该方向是相通的,可对数据进行大胆的假设。 对照表四,(6,5)是未探测过的,其值为FFH,分析与之相邻的(5,5)(7,5)和(6,6)(6,4)二组数据,(6,4)的数据为FFH,放弃在南北方向上的补全,考虑东西方向,(5,5)向东是可行的,(7,5)向西是可行的,因而可以大胆设想,(6,5)是东西可行的,数据可设为60H,将60H填入表四,就得到补全后的表五。 表五 补全后的二维表 2.6 等高表 经过有限次的探测、阻断与补全后,已经可以得到描述迷宫图线路的二维表,虽然不是全部,但已经是部分或大部分,其中可能包含了若干条可以到达终点的路径,为了寻找到达终点的路径,需要制作等高表。等高表是指已探测的各单元距离起点的步数(一个单元为一步),起点的步数为0,表六为通过表五所获得的等高表。等高值以十进制数表示。 表六 等高表 2.7 可行路径 在等高表中,可行路径上任一单元到起点的步数都是已知的,按从大到小的次序,可以返回起点。按从小到大的次序,可到达终点,这样的可行路径可能不止一个,而是多个。可行路径的查找,从起点开始,在允许前进的方向上,按比当前等高值高1的方向前进,直到终点。有时可能会遇到下一单元的等高值小于当前值(如(6,2)点)或比当前值高1以上的情况,如果当前单元不是交叉点,可以不予理会,进入下一个单元,按等高值增加的方向查找。如果是交叉点,则要进行趋势分析,找出等高值就增加的方向。舍弃等高值减少的方向。 图七 是根据表六得到的所有可行路径,共有A、B、C、D四条。 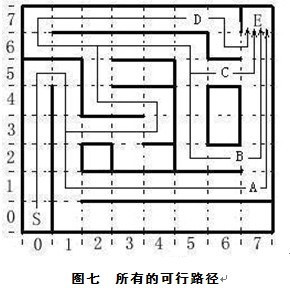
图七 所有的可行路径2.8 可行路径的步数 可行路径的步数,指由起点到达终点,所经过的单元数,可由等高表计算得出。 线路A:由(0,0)到(7,4),19步,(7,4)到(7,5)1步,(7,5)到(7,6)1步,(7,6)到(7,7),28-27=1步。总计=19+1+1+1=22步。 线路B:由(0,0)到(6,2),24步,(6,2)到(7,2)1步,(7,2)到(7,4),19-17=2步,(7,4)到(7,5),1步, (7,5)到(7,6),1步。(7,6)到(7,7),28-27=1步,总计=24+1+2+1+1+1=30步。 同理可得线路C:22+1+1=24。线路D:28。 2.9 最佳路径 电脑鼠要在最短的时间内完成由起点到终点的冲剌,路径的选择至关重要,步数少的路径,是最佳路径的条件之一,但不是唯一条件。考虑电脑鼠在拐弯时,同样需要时间,所以要对拐弯次数加权后加到步数中得到加权步数。 加权步数=步数+拐弯次数×拐弯权重 拐弯次数:一个90度的拐弯算一次,一个180度的拐弯算二次。 拐弯权重:这是一个对结果有重要影响的参数,要结合电脑鼠的结构和试跑确定。如果电脑鼠无加速功能,是以恒速前进,其值可选0.4~1.0之间,如果电脑鼠有变速功能,可根据变速的范围,其最值可适当增加。表7与表8,分别列出了不同的拐弯权重,对加权步数的影响。 表七 拐弯权重为0.5时,各线路的加权步数 表八 拐弯权重为1.5时,各线路的加权步数 从表七与表八中,已经明显看出了拐弯权重对加权步数的影响,线路B与线路D的排名次序发生了逆转。 3 结论 本文详细介绍了一种电脑鼠走迷宫的算法,实践表明该算法可以基本满足电脑鼠走迷宫竞赛的要求。电脑鼠走迷宫已有的算法很多,新算法也层出不穷。本文仅为抛砖引玉,以供同行参考。 |