本帖最后由 旭日东升 于 2012-4-16 21:52 编辑
4.NXTway-GS 控制部分设计 本章介绍NXTway-GS基于现代控制理论的控制器设计（两轮倒立摆）。
4.1控制系统 控制系统的特性包括以下几点：
输入和输出
尽管在方程（3.31）输入u为电压，实际输入的是通过PWM占空比完成左右两边的直流电动机的控制输入。传感器的输出是直流电动机角θml,r和身体的俯仰角速度ψ。
图4-1 输入和输出
这是很容易通过评估θ，φ的θml,r ，通过 有两种方法来评估ψ。
1． 积分角速度数值推导出ψ
2． 采用基于现代控制理论中的一个参量估计ψ
我们使用方法1完成下面控制器设计。
稳定稳定性
这是很容易理解NXTway-GS平衡位置并不稳定。我们需要保持同一方向的车身仰角情况下，NXTway-GS才能保持平衡。现代控制理论提供了许多技术
来实现一个稳定的系统。 （见附录A）
4.2 控制器设计
方程（3.29）类似质量 - 弹簧 - 阻尼系统的力学方程。图4-2显示了两轮倒立摆的解释为质量 - 弹簧 - 阻尼系统的等效系统图。
图4-2质量 - 弹簧 - 阻尼系统图 我们发现我们可以通过调整如图4-2所示的弹簧常数和阻尼摩擦常数来使两轮倒立摆稳定。这样可以利用附录中所述的控制理论中方法来计算这些常数。
我们使用附录A.3提到的伺服控制器完成NXTway-GS控制器并且选择θ作为伺服控制器参考。重要的是我们使用θ作为参考，同θ相比不能使用其他变量，否则系统将变得无法控制。图4-3展示了NXTway-GS伺服控制器框图。
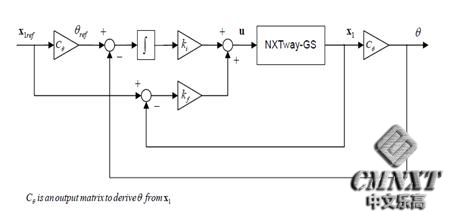
图4-3 NXTway-GS伺服控制器框图 通过线性二次调节方法,我们计算反馈增益和积分增益。我们选择由实验性的试验和误差得来的下面权重矩阵Q和R。
Q（2,2）是车身俯仰角的权重设置，Q（5,5）是测量平均角度和参考角度之间的差异时间累加的权重。
param_controller.m完成LQR（线性二次型调节）计算，并定义其他参数。它的增益计算部分源代码如下：
其计算结果如下：
k f =[-0.8351, - 34.1896, - 1.0995, ki = -0.4472 因为NXTway-GS的过度波动,我们调整线性二次型调节速度增益kf(3)计算后的值。
更多我们添加下面控制
@ 旋转NXTway-GS通过不同的左右马达转速
@ 当NXTway-GS需要直线前行时，由于直流电动机的旋转角度是不一样的，即使相同的PWM时，也需要通过比例器控制两个轮子同步
因此我们推导出如图4-4所示NXTway-GS控制器。
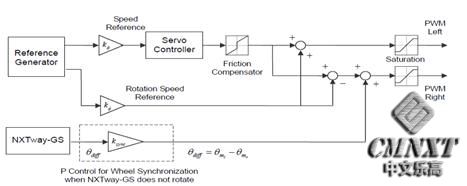
图4-4NXTway-GS控制器框图 | 
IP卡
狗仔卡
发表于 2012-4-12 23:25:44
提升卡
置顶卡
沉默卡
变色卡
千斤顶
显身卡
发表于 2012-4-13 00:15:33
